The value of being indispensable
A cooperative approach to bargaining with a continuum of players
My PhD resesarch project examines the applicability of random order values, and more specifically, the Shapley value to the problem of modeling bargaining in a setting with one indispensable player and a large number of smaller, non-indispensable players. The project is motivated by platform economies, but the results are applicable to a wide range of settings. The repository for the thesis, as well as the three chapters, can be found at stanmart/phd-thesis.
The chapter is an abstract, theoretical treatment of the problem.
- Paper: The value of being indispensable: A cooperative approach to bargaining with a continuum of players
- Archived Github repository: stanmart/ValueOfIntermediation
The value of being indispensable: a cooperative approach to bargaining with a continuum of players
This paper investigates the idea of using random order values, a concept from cooperative game theory, to model bargaining outcomes in games with one indispensable player and a continuum of fringe players. I show that this approach proves to be very tractable, and leads to results that are in line with one’s intuitive expectations about bargaining outcomes. Thus, it can be a useful tool in modelling situations where one does not want to attribute all the bargaining power to one side of the market, and at the same time would like to avoid having to deal with an explicit multi-stage bargaining game.
The bargaining outcomes in the simplest model (Shapley value, one indispensable big player, non-heterogeneous fringe players) also have a nice, intuitive graphical representation. Imagine that the big player and \(t\) fraction of the fringe players can generate \(f(t)\) total value. Then, the total value can be represented by a rectanle with width 1 and height \(f(1)\). It turns out, that the big player gets the area of this rectangle which is below the graph of \(f(t)\), while the fringe players share ther est equally.
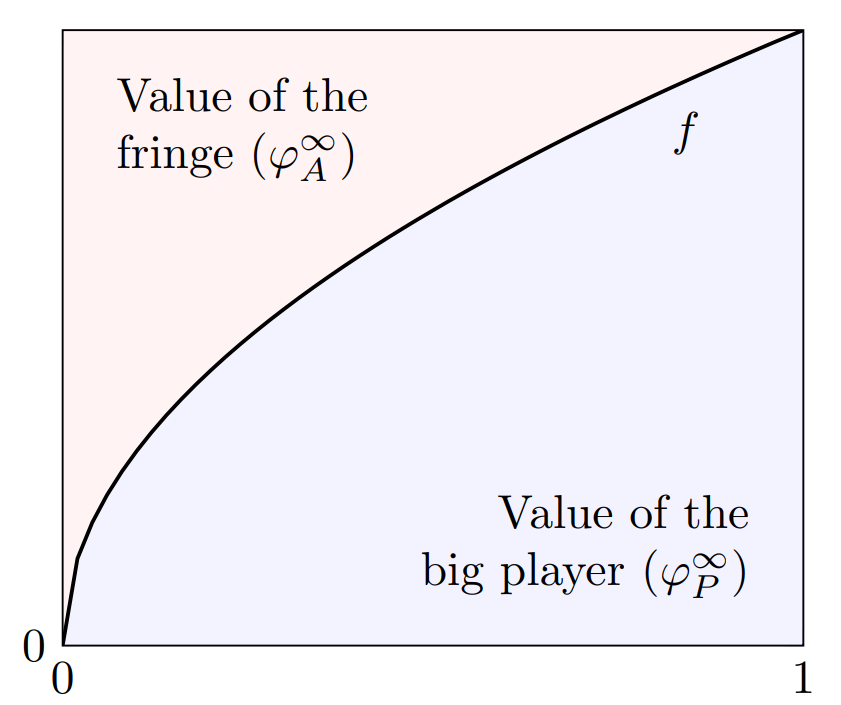
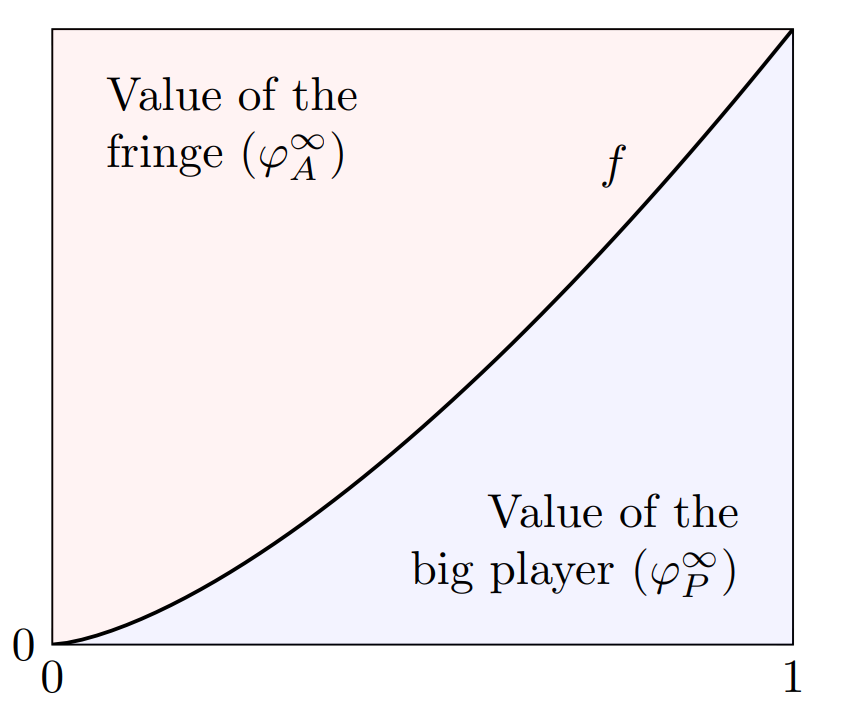
This captures the idea that the bargaining position of the big player is better when it is less important to have all fringe players on board, i.e. fringe players are more substitutable in a sense.
The paper contains a number of more general results, such as:
- Non-symmetric values
- Heterogeneous fringe players
- Not totally indispensable big player(s)
The aim of the paper is to provide a tool-kit for including bargaining into more complex models in a tractable way. For this purpose, the paper also contains a short example application to provide an example of how the results can be used in practice.